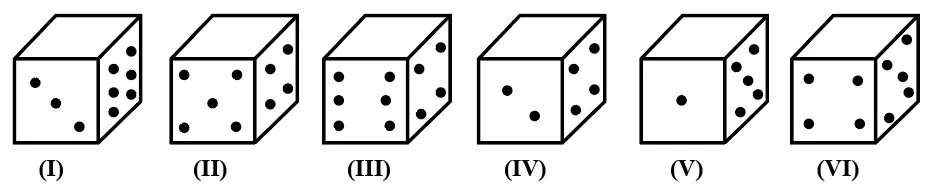IPMAT Rohtak 2020 (LR) - The sum of the numbers of dots on the opposite face is 7. If the odd numbered dice have even number of dots on their top faces, then what would be the total number of dots on the top faces of their dice? | PYQs + Solutions

IPMAT Rohtak 2020

Logical Reasoning

Medium

Eight

Ten

Twelve

Fourteen

✅ Correct Option: 1

Related questions:

A cube has six numbers marked $1,2,3,4,5$ and 6 on its faces. Four views of the cube are shown below :

What is the number on the face opposite to the face showing 4 ?

Choose the box that is similar to the box formed from the given sheet of paper (X).

A cube is coloured red on all of its faces. It is then cut into 64 smaller cubes of equal size. Which of the following statements are correct?

(A) The number of smaller cubes with two surfaces painted is 36.

(B) The number of smaller cubes with one surface painted is 24.

(D) The number of smaller cubes with at least two surfaces painted is 30.

IPMAT Rohtak 2020 (LR) PYQs