IPMAT Indore 2022 (MCQ) - The curve represented by the equation x^2 sqrt(2)- sqrt(3)+y^2 sqrt(2)- sqrt(3)=1 is | PYQs + Solutions

IPMAT Indore 2022

Geometry

Conic Sections

Medium

The curve represented by the equation $\dfrac{x^{2}}{\sin \sqrt{2}-\sin \sqrt{3}}+\dfrac{y^{2}}{\cos \sqrt{2}-\cos \sqrt{3}}=1$ is

an ellipse with the foci on the y-axis

an ellipse with the foci on the x-axis

a hyperbola with the foci on the x-axis

a hyperbola with the foci on the y-axis

Correct Option: 1

General form of an Ellipse:

\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1

, where both

a

and

b

should be positive.

If:

\newline

\rarr a>b

, then the foci lies on the

x

-axis.

\newline

\rarr b>a

, then the foci lies on the

y

-axis.

We know that:

\newline

\pi^{c}

(radians) =

180{\degree}

\Rightarrow 1^{c}=\dfrac{180}{22} \times 7

= 57.27{\degree}

\dfrac{x^2}{\sin \sqrt 2 - \sin \sqrt3}+\dfrac{y^2}{\cos \sqrt2 - \cos \sqrt3}=1

Here,

\sqrt 2

and

\sqrt 3

are in radians. Let's convert them into degrees.

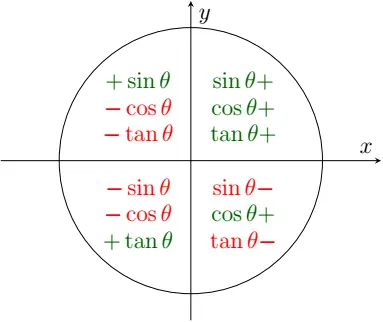\Rightarrow \dfrac{x^2}{\sin (1.414 \times 57.27) - \sin (1.732 \times 57.2)}+\dfrac{y^2}{\cos (1.414 \times 57.27) - \cos(1.73 \times 57.2) }=1

\dfrac{x^2}{\sin (80.99) - \sin (99.19) }+\dfrac{y^2}{\cos (80.99) - \cos (99.19)}=1

As per the trigonometric quadrant rule, the value of

\sin (80.99)

is positive [

\because 80.99

lies in the first quadrant] and so is

\sin (99.19)

[

\because 99.19

lies in the second quadrant].

Also,

\cos (80.99)

is positive [

\because 80.99

lies in the first quadrant] and

\cos (99.19)

is negative [

\because90.99

lies in the second quadrant].

\therefore (\cos (80.99) - \cos (99.19))

is positive.

Note that the value of

\sin (80.99)

is greater than that of

\sin (99.19)

. How?

\newline

The maximum value that

\sin \theta

can take is

1

when

\theta = 90{\degree}

. The angle

80.99

is closer to

90

in comparison to

99.19

. Hence, the former is greater than the latter and their difference will be positive.

As both

a

and

b

are positive, the given curve is an Ellipse.

\newline

Also, as

a

is the difference of two values and

b

is the sum of two values, we can say that

b > a

. Therefore, the foci of this ellipse lies on the

y

axis.

Hence, answer is option (a).

IPMAT Indore 2022 (MCQ) PYQs

The curve represented by the equation x2sin⁡2−sin⁡3+y2cos⁡2−cos⁡3=1 \dfrac{x^{2}}{\sin \sqrt{2}-\sin \sqrt{3}}+\dfrac{y^{2}}{\cos \sqrt{2}-\cos \sqrt{3}}=1 sin2​−sin3​x2​+cos2​−cos3​y2​=1 is

Keyboard Shortcuts

The curve represented by the equation $\dfrac{x^{2}}{\sin \sqrt{2}-\sin \sqrt{3}}+\dfrac{y^{2}}{\cos \sqrt{2}-\cos \sqrt{3}}=1$ is