IPMAT Indore 2022 (MCQ) - For 0/4, let a=(( )^ )( _2 ), b=(( )^ )( _2 ), c=(( )^ )( _2 ) and d=(( )^ )( _2 ). Then, the median value in the sequence a, b, c, d is | PYQs + Solutions

IPMAT Indore 2022

Geometry

Trigonometry

Hard

For $0\lt\theta\lt\frac{\pi}{4}$ , let $a=\left((\sin \theta)^{\sin \theta}\right)\left(\log _{2} \cos \theta\right), b=\left((\cos \theta)^{\sin \theta}\right)\left(\log _{2} \sin \theta\right), c=\left((\sin \theta)^{\cos \theta}\right)\left(\log _{2} \cos \theta\right)$ and $d=\left((\sin \theta)^{\sin \theta}\right)\left(\log _{2} \sin \theta\right)$ . Then, the median value in the sequence $a, b, c, d$ is

\frac{a+b}{2}

\frac{a+d}{2}

\frac{b+c}{2}

\frac{c+d}{2}

Correct Option: 2

In the graph given below, the green line shows the sine curve and the blue line shows the cosine curve.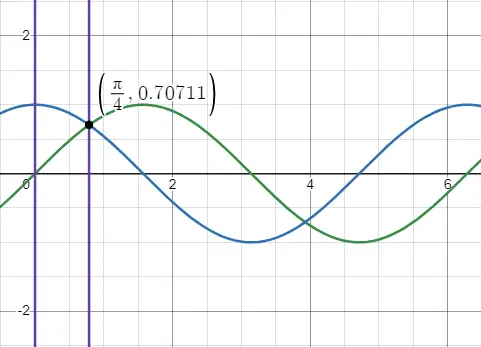

By closely looking at the graph, we can conclude that for

0< \theta < \dfrac{\pi}{4}

, the value of

\cos \theta

will be higher than the value of

\sin \theta

To make our calculations slightly easier, let us assume some values for

\sin \theta

and

\cos \theta

Let:

\sin \theta = 0.01

and

\cos \theta = 0.1

\Rightarrow \dfrac{a}{b} = \dfrac{(0.01)^{0.01}}{(0.1)^{0.01}} \times \dfrac{\log_2 0.1}{\log_2 0.01}

\Rightarrow (\dfrac{0.01}{0.1})^{0.01} \times \log_{0.01} 0.1

[

\because \dfrac{\log a}{\log b} = \log_b a

]

\Rightarrow (\dfrac{1}{10})^{0.01} \times (\dfrac{-1}{-2}) \log_{10} 10

[

\because \log_{m^b} n^a = \dfrac{a}{b} \log_m n

]

\Rightarrow \dfrac{a}{b} = (\dfrac{1}{10})^{0.01} \times \dfrac{1}{2}(1)

[

\because \log_a a = 1

]

\newline

or,

\dfrac{a}{b} = \dfrac{1}{10^{0.01}} \times \dfrac{1}{2}

\therefore b > a

Using the same approach, we'll compare

c

and

d

\Rightarrow \dfrac{c}{d} = \dfrac{(0.01)^{0.1}}{(0.01)^{0.01}} \times \dfrac{1}{2}

\Rightarrow \dfrac{c}{d} = (0.01)^{0.1-0.01} \times \dfrac{1}{2}

\Rightarrow \dfrac{c}{d} = (\dfrac{1}{100})^{0.09} \times \dfrac{1}{2}

\therefore d > c

Similarly, comparing

b

and

d

, we get

b > d

\because b > a, d > c

and

b > d

, it can be said that

b

is the greatest among all.

Now comparing

a

and

c

, we get

a > c

. Thus,

c

is the smallest value among all.

The 'median' of a sequence is the middle-most value, given that the sequence is arranged in an ascending order.

b

(the greatest value) and

c

(the smallest value) will occupy the extreme positions when arranged in an increasing order. In other words, they cannot occupy the positions in the middle.

Hence,

a

and

d

will occupy the middle positions.

IPMAT Indore 2022 (MCQ) PYQs

Keyboard Shortcuts