JIPMAT 2022
Geometry
Circles
Medium
If the radius of each of four outer circles is , then the radius of the innermost circle is 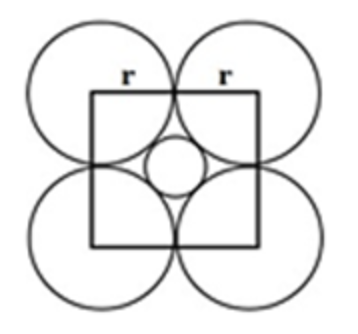
If the radius of each of four outer circles is , then the radius of the innermost circle is 
Correct Option: 3
1) In this figure, the four outer circles of radius are arranged around a square touching the innermost circle.2) Consider half of the square's diagonal: - It connects the center of the innermost circle to the corner of the square - Also equals the radius we're looking for plus the side of the square3) Let radius of innermost circle be Side of square = (since small circle touches sides of square)4) Due to symmetry, centers of large circles form a square of side 5) From Pythagorean theorem: 6) Solving quadratic equation: Therefore, radius of innermost circle is
Related questions:

